theoretical probability vs experimental probability of a casino roulette 25/01/2025,experimental probability examples,theoretical probability vs experimental probability of a casino roulette,It is helpful to find the probability of the expected event to occur at least a certain number of times after n spins. Because events are mutually exclusive, we can add their probabilities to find the Here’s what you can expect to find at the best online casino sites in Asia. Table games: include variants of baccarat , roulette , blackjack , craps, and poker. Slots : this is probably the most .

Introduction:
A probability model starts from an experiment and a mathematical structure attached to that experiment, namely the field of events. The event is the main unit probability theory works on. In gambling/online gambling, there are many categories of events, all of which can be textually
Understanding the difference between experimental and theoretical probability equips you with valuable insights for making informed decisions. While experimental probability relies on actual data from observations or experiments, theoretical probability is based on mathematical calculations and assumptions. In the context of a casino roulette, these concepts play a crucial role in analyzing the game's outcomes and determining the fairness of the game. In this article, we will explore the theoretical and experimental probabilities of a casino roulette, providing examples, discussing real-life applications, explaining the mathematics behind roulette, and comparing theoretical and experimental probability formulas. By the end, you will have a comprehensive understanding of the theoretical and experimental probabilities associated with casino roulette.
Experimental Probability Examples:
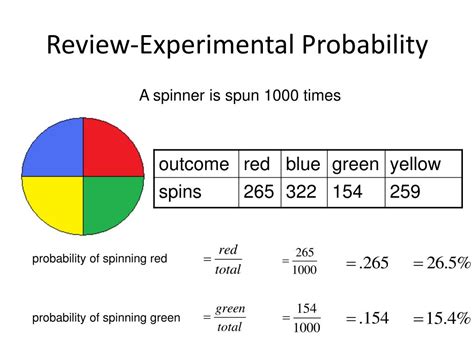
To better comprehend experimental probability, it is essential to consider some examples. Imagine you are observing a roulette table in a casino and recording the outcomes of 100 spins. If you count the number of times the ball lands on a red number, let's say it occurs 45 times out of the 100 spins. In this case, the experimental probability of the ball landing on a red number can be calculated by dividing the number of favorable outcomes (45) by the total number of outcomes (100). Therefore, the experimental probability of landing on red is 45/100, which simplifies to 0.45 or 45%.
Similarly, if you observe the ball landing on an even number 30 times out of the 100 spins, the experimental probability of landing on an even number can be calculated as 30/100, which simplifies to 0.3 or 30%. These experimental probabilities provide a snapshot of the outcomes based on the observed data.
Experimental Probability in Real Life:
Experimental probability is not limited to casino games like roulette but can also be applied to various real-life situations. For example, consider a survey conducted to determine the probability of people owning a smartphone. A random sample of 500 individuals is selected, and out of those, 400 individuals own a smartphone. The experimental probability of owning a smartphone can be calculated as 400/500 or 0.8, which means that 80% of the sampled population owns a smartphone.
Similarly, experimental probability can be applied in fields like medicine, economics, and sports. In medicine, clinical trials are often conducted to analyze the effectiveness of a new drug. The experimental probability of the drug producing a desired outcome can be calculated by dividing the number of patients who experienced positive results by the total number of patients in the trial.
How is Experimental Probability Used?
Experimental probability is widely used in various fields to analyze and predict outcomes based on observed data. In the context of a casino roulette, it can be used to determine the fairness of the game. By observing the number of times the ball lands on specific numbers or colors, players can make informed decisions on how to place their bets.
For instance, if a player notices that the ball has landed on a black number more frequently than a red number, they may decide to place more bets on black for the next few spins, assuming that the trend will continue. This strategy is based on the experimental probability derived from their observations. However, it is important to note that experimental probability is not foolproof and should be used with caution, as it is subject to random variations and limited sample sizes.
The Mathematics of Roulette:
To understand the theoretical probability of a casino roulette, it is crucial to delve into the mathematics behind the game. A standard roulette wheel consists of 36 numbers, alternating between red and black, with an additional two green numbers (0 and 00) in American roulette. The theoretical probability of the ball landing on any specific number is 1/38 or approximately 0.0263 in American roulette. In European roulette, which does not have the double zero, the theoretical probability becomes 1/37 or approximately 0.0270.
Similarly, the theoretical probability of the ball landing on red or black is 18/38 or approximately 0.4737 in American roulette, and 18/37 or approximately 0.4865 in European roulette. These probabilities are derived from the assumption that the roulette wheel is perfectly balanced, and each number has an equal chance of being selected.
Theoretical vs Experimental Probability Formula:
Theoretical probability can be calculated using a simple formula. For a specific outcome, the theoretical probability is equal to the number of favorable outcomes divided by the total number of possible outcomes. In the case of a casino roulette, the total number of possible outcomes is 38 in American roulette and 37 in European roulette.
On the other hand, experimental probability is calculated by dividing the number of favorable outcomes observed in a given experiment by the total number of trials or observations. This formula allows us to estimate the probability based on real data.
To summarize, here are the formulas for theoretical and experimental probability:
Theoretical Probability Formula:
P(A) = Number of favorable outcomes / Total number of possible outcomes
Experimental Probability Formula:
P(E) = Number of favorable outcomes observed / Total number of trials or observations
What is a Theoretical Probability?
Theoretical probability refers to the probability of an event occurring based on mathematical calculations and assumptions. It provides an idealized representation of the probability, assuming that all outcomes are equally likely. In the context of a casino roulette, theoretical probability is determined by the design of the wheel, where each number has an equal chance of being selected.
However, it is important to note that theoretical probability does not always align with the actual outcomes observed in real-life scenarios. This is where experimental probability comes into play, allowing us to compare and contrast the theoretical expectations with the actual results.
Conclusion:
Understanding the concepts of theoretical and experimental probability is essential when analyzing the outcomes of a casino roulette. While theoretical probability is based on mathematical calculations and assumptions, experimental probability relies on actual data from observations or experiments. By comparing the theoretical and experimental probabilities, players can make informed decisions when betting on the roulette table.
Understanding the difference between experimental and theoretical probability equips you with valuable insights for making informed decisions. While experimental probability relies on actual …
theoretical probability vs experimental probability of a casino roulette 25/01/2025 NBA schedule, results of 2024-25 season games airing in the Philippines The NBA 2024-25 season is in full swing! Check out the schedule of games airing in the Philippines--particularly NBA TV Philippines and Pilipinas Live.
theoretical probability vs experimental probability of a casino roulette - experimental probability examples